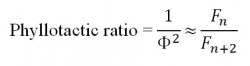Phyllotaxis: The Fibonacci Sequence in Nature
Divergence Angles and Phyllotactic Ratios
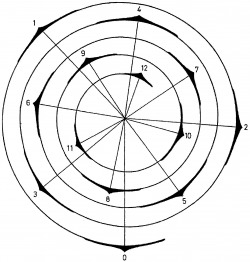
The term phyllotaxis means “leaf arrangement” in Greek and was coined in 1754 by Charles Bonnet, a Swiss naturalist (Livio “Story,” 109). In the 1830s, a pair of scientist brothers found that each new leaf on a plant stem is positioned at a certain angle to the previous one and that this angle is constant between leaves: usually about 137.5 degrees. “That is, if you look down from above on the plant and measure the angle formed between a line drawn from the stem to the leaf and a corresponding line for the next leaf, you will find that there is generally a fixed angle, called the divergence angle” (Tung 13).
Assuming that the sun and rain come from above, orthogonal (perpendicular) to the plane of the leaf, the divergence angle must be such as to minimize blockage of lower leaves by higher leaves. Therefore, any sort of periodic leaf arrangement must be avoided, if possible, as this will result in such blockage. So, the most optimal arrangement is obtained if we divide the circle formed by the plant (i.e. in the image above) by an irrational number–the more irrational the better. Earlier, we determined that the golden ratio is the most irrational number, and therefore we arrive at a divergence angle of 360/(phi) = 222.5, or, equivalently, 360-222.5 = 137.5 degrees, which is the most prevalent angle observed (Tung 14).
“Botanists define the phyllotactic ratio as the fraction of a circle through which a new leaf turns from the previous (older) leaf” (Tung 14). In the case of a 137.5-degree divergence angle, the ratio is 1/phi, which is approximately 0.618, as we saw here. Since this is over half of the circle, we subtract this from one to get 1/(phi^2), or about 0.382. In approximating this rationally, we arrive at the ratio of two Fibonacci numbers:
So, we can see that as the number of leaves approaches infinity (which implies that n approaches infinity) the phyllotactic ratio becomes a better and better approximation of 1/(phi^2). However, all of these claims are made on the basis of two assumptions. First, that the plants have infinite leaves, and, second, that maximum sun exposure is the only factor that determines leaf placement. Neither of these apply, but a divergence angle of 137.5 degrees is still most commonly observed in nature (Tung 14-15)
Examples of Golden Ratio-Based Phyllotaxis.
Now that we have explored the theory of phyllotaxis based on phi, let us now consider various examples in which this actually occurs.
First, the pineapple. Each scale on the fruit is a hexagon and is part of three different spirals along the rind.
In the image above, there are eight gently-sloping spirals (left), thirteen steeper spirals (middle), and twenty-one very steep spirals. “Most pineapples have five, eight, thirteen, or twenty-one spirals of increasing steepness on their surface. All of these are Fibonacci numbers” (Livio “Story,” 111).
We now turn our discussion to the sunflower, in which one can observe two families of spiral patterns: one winding clockwise and the other counterclockwise. The quantity of spirals in each family are always two consecutive Fibonacci numbers. This effect is the result of closely packing points separated by 137.5 degrees in tight spirals. This implies that the a golden-ratio based phyllotaxis allows not only for optimal sun exposure but also for maximal packing in horizontal space.
The petal count of field daisies is usually either thirteen, twenty-one, or thirty-four petals, all consecutive Fibonacci numbers. The seed head also consists of the above-mentioned Fibonacci spirals. Pinecones also exhibit these spiral patterns, as seen below (Livio “Story,” 113).
The Dynamical Model
Research (by Coxeter, Adler, and Rivier, cited in Livio “Story” 113) has shown that buds placed along a spiral and separated by an angle of 137.5 degrees (known also as the golden angle) are packed most effienciently along the spiral. in 1868, Wilhelm Hofmeister suggested that new primordia (i.e., cells that will later develop into leaves, petals, etc.) always form in the least crowded spot along the growing tip of a plant (called a meristem). This is now known as Hofmeister’s rule (Tung 21).
Because the plant is continuously growing, each successive primordium forms at one point along the meristem and then moves radially outward at a rate proportional to the stem’s growth. Hofmeister’s rule tells us that the second primordium is placed as far as possible from the first, and the third is placed at a distance farthest from both the first and the second primordia. As the number of primordia increases, the divergence angle eventually converges to a constant value of 137.5 degrees and thus creates Fibonacci spirals (Tung 20-21). However, this model is simply that: a model. “Consequently, the phyllotaxis rules I have described cannot be taken as applying to all circumstances, like a law of nature. Rather, in the words of the famous Canadian mathematician Coxeter, they are ‘only a fascinatingly prevalent tendency” (Livio “Story,” 115).